∃x ∈ ]a, b[, Q1 > 0 and ... Qk > 0

In order to understand the idea, we will consider the easier formula ∃x ∈ ]a, b[, P > 0 and Q > 0. We replace it by the disjunction of the following formulas.
  1. (∀x ∈ ]a, b[, P > 0) and
    (∀x ∈ ]a, b[, Q > 0)
    Either P and Q are strictly positive over all ]a, b[.
  2. ∃u ∈ ]a, b[,( ∀x ∈ ]u, b[, P > 0)  and
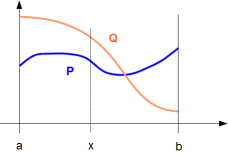
    ( ∀x ∈ ]u, b[, Q > 0)  and
    [P(u) = 0 or Q(u) = 0]
    Or P and Q are only strictly positive over an interval ]u, b[.
    But in this case, if we take u such that ]u, b[ is the greatest interval such that P and Q are only strictly positive over it, then either P(u) = 0 or Q(u) = 0.
    Indeed, if not, either P(u) > 0 and P(u) > 0 but in this case, ]u, b[ is NOT the greatest interval such that P and Q are only strictly positive over it.
    Or either P(u) < 0 or Q(u) < 0.
    But this is not possible because P and Q are continuous fonction ;

  3. ∃v ∈ ]a, b[, (∀x ∈ ]a, v[, P > 0) and
    (∀x ∈ ]a, v[, Q > 0)  and
    [P(v) = 0 or Q(v) = 0]
    Or P and Q are only strictly positive over an interval ]a, v[ and P(v) = 0 or P(v) = 0
  4. ∃u, v ∈ ]a, b[, (∀x ∈ ]u, v[, P > 0)  and
    (∀x ∈ ]u, v[, Q > 0)  and
    [P(u) = 0 or Q(u) = 0] and
     [P(v) = 0 or Q(v) = 0]
    Or P and Q are only strictly positive over an interval ]u, v[ and [P(u) = 0 or P(u) = 0] and [P(v) = 0 or P(v) = 0]