Objectives and scientific standpoint

The OATMIL project will propose novel concepts, methodologies, and new tools for exploiting large data collections. This will result from a cross-fertilization of fundamental tools and ideas from optimal transport (OT) and machine learning (ML)

Optimal transport

Introduced by Gaspard Monge in the 19th century, optimal transport (OT) reappeared in the work of Kantorovitch and recently found surprising new developments in a wide range of fields, including computational fluid mechanics, color transfer between multiple images or warping in the context of image processing, interpolation schemes or distance computation on meshes in computer graphics, and economics, via matching and equilibrium problems. Fundamentally, OT provides means of defining distances between probability measures defined in potentially high-dimensional metric spaces. These distances, which have received several names in the literature (Wasserstein, Monge-Kantorovich or Earth Mover distances), have strong and important properties: i) they can be evaluated when only empirical measures of the distributions are observed, and do not require estimating parametric or semi-parametric distributions as a preprocess; ii) they can exploit the geometry of the underlying metric space, and provide meaningful distances even when the supports of the distributions do not overlap.

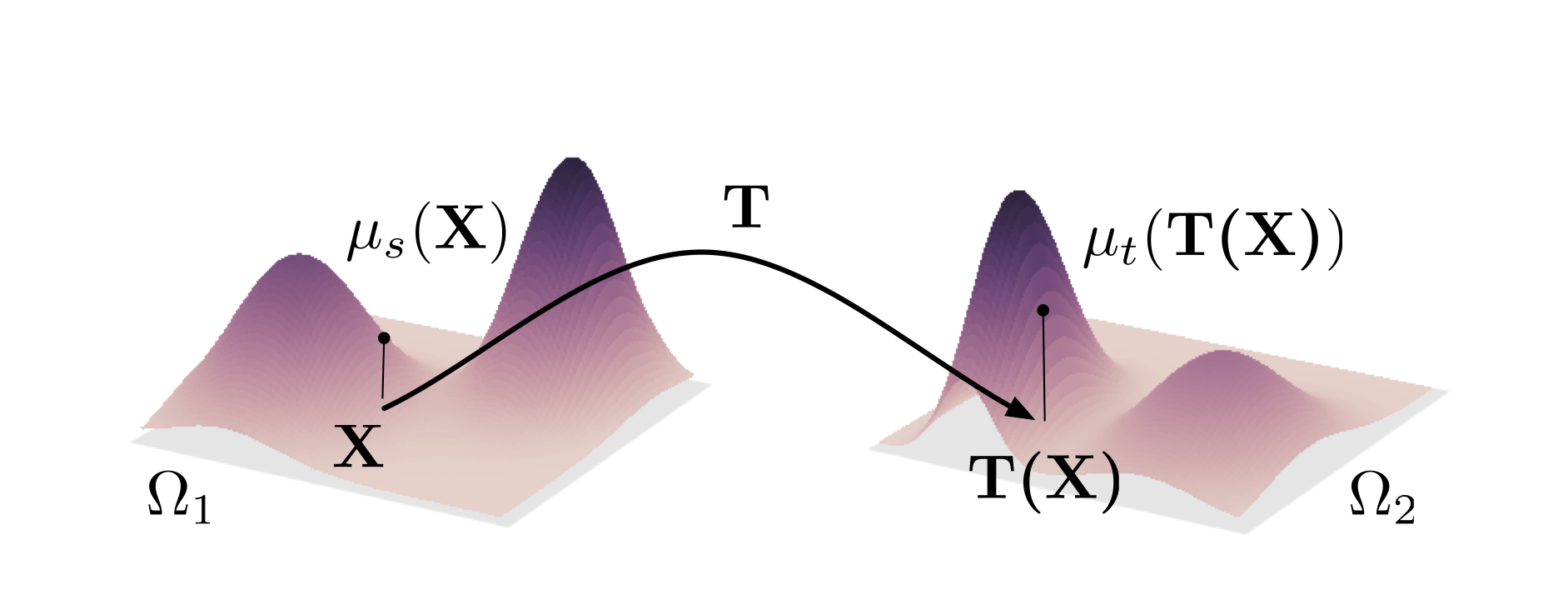
ML exploits the empirical distribution of some training data to adapt the parameters of certain algorithms (classifiers, regressors, etc.) and perform some prescribed tasks. While computing dis- tances between (empirical) probabilities is very appealing for ML, the use of OT distances is still in its infancy mainly due to the high computational cost induced by solving for the optimal transportation plan. Recently, new computing strategies have emerged (such as entropy-regularized or Sinkhorn transport) that turn OT distances into more tractable tools. ML applications are emerging for complex problems such as domain adaptation, semi-supervised learning, factorial analysis or as data fitting term for multiclass classifiers.

Main objectives and research hypothesis

The main objective of OATMIL is to develop new techniques for large-scale machine learning, encompassing adaptability, scalability, and robustness, by a cross-fertilization of ideas coming from OT and ML. This cross-fertilization leads to two complementary scientific challenges : bringing OT to ML and bringing ML to OT, which we discuss in more details below.

1. Bringing OT to ML: our vision is that it is possible to develop new innovative machine learn- ing methodologies by leveraging fundamental advances in OT. We will primarily focus on three different subjects of interest that relate to fundamental problems in machine learning:
   • domain adaptation and transfer learning, where OT will be used to measure the discrepancy between (possibly multiple) domains or tasks. Then, new learning methods can be devised that exploit efficiently this measure to perform adaptation. A specific focus will also be given to heterogeneous domain adaptation,
   • distances over structured data, where OT will be used to measure similarities on graphs, trees or time-series, empowering new distances between structured data. The key problem here is to find efficient methods and algorithms to incorporate the structure in the geometry of the transport, and
   • factorization and coding, OT being used as a data-fitting loss functions in estimation prob- lems, where data can be interpreted as distributions (e.g power spectral density, spectral data).
2. Bringing ML to OT: we strongly believe that advances in large scale ML optimization can help addressing well known numerical bottlenecks of OT. We will design efficient numerical tools to compute OT plans possibly associated to new regularization strategies fitting the machine learning needs. Our approach will be based on three complementary pillars:
   • dimension-reduction with sketching strategies to compress the empirical distribution of large-scale collections using a few nonlinear moments. Recent work has established PAC (probably approximately correct) bounds for certain learning tasks, and a particular challenge will be to extend this to the desired OT problems.
   • dedicated optimization schemes will be devised and adapted to fit the problem specificities: We envision to investigate fast stochastic/incremental optimization methods that efficiently handle the geometrical structure of bi-stochastic constraints or cutting-planes-like algorithms that relax constraints and gradually tighten them.
   • stochastic and online optimization strategies will be investigated for large OT problems, that will notably allow to consider OT as a new building brick for deep learning architectures. More specifically we plan to learn explicit transport maps instead of relying on probabilistic couplings.

Publications

• Courty, N., Flamary, R., Habrard, A., Rakotomamonjy, A. 2017, 'Joint Distribution Optimal Transportation for Domain Adaptation', arXiv:1705.08848, accepted for publication at NIPS 2017
• Courty, N., Flamary, R., Ducoffe, M. 2018, 'Learning Wasserstein Embeddings', https://openreview.net/forum?id=SJyEH91A-, accepted for publication at ICLR 2018
• V. Seguy, B. Bhushan Damodaran, R. Flamary, N. Courty, A. Rolet, M. Blondel 2018, 'Large-Scale Optimal Transport and Mapping Estimation', https://openreview.net/forum?id=B1zlp1bRW, accepted for publication at ICLR 2018
• B. Kellenberger, D. Marcos, N. Courty, D. Tuia. Detecting Animals in Repeated UAV Image Acquisitions by Matching CNN Activations with Optimal Transport, accepted for publication at IGARSS 2018 https://hal.archives-ouvertes.fr/hal–02174328
• B. Damodaran, B. Kellenberger, R. Flamary, D. Tuia, N. Courty. DeepJDOT: Deep Joint Distribution Optimal Transport for Unsupervised Domain Adaptation, accepted for publication at ECCV 2019 https://hal.archives-ouvertes.fr/hal–01956356
• R. Flamary, M. Cuturi, N. Courty, A. Rakotomamonjy. Wasserstein Discriminant Analysis. Machine Learning, Springer Verlag, 2018 https://hal.archives-ouvertes.fr/hal–02112754
• T. Vayer, R. Flamary, R. Tavenard, L. Chapel, N. Courty. Sliced Gromov–Wasserstein, accepted for publication at NeurIPS 2019
• T. Vayer, L. Chapel, R. Flamary, R. Tavenard, N. Courty. Optimal Transport for structured data with application on graphs, accepted for publication at ICML 2019
• Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia 2019, 'Optimal Transport for Multi-source Domain Adaptation under Target Shift', arXiv:1803.04899, accepted for publication at AISTATS 2019
• Bharath Bhushan Damodaran, Rémi Flamary, Viven Seguy, Nicolas Courty. An Entropic Optimal Transport Loss for Learning Deep Neural Networks under Label Noise in Remote Sensing Images. 2019. ⟨hal–02174320⟩. Accepted for publication in CVIU
• Titouan Vayer, Rémi Flamary, Romain Tavenard, Laetitia Chapel, Nicolas Courty. Sliced Gromov–Wasserstein. NeurIPS 2019 – Thirty–third Conference on Neural Information Processing Systems, Dec 2019, Vancouver, Canada. ⟨hal–02174309⟩
• ALAYA, Mokhtar Z., BERAR, Maxime, GASSO, Gilles, et al. Screening sinkhorn algorithm for regularized optimal transport. NeurIPS 2019 – Thirty–third Conference on Neural Information Processing Systems, Dec 2019, Vancouver, Canada. arXiv preprint arXiv:1906.08540
• Antoine Ackaouy, Nicolas Courty, Emmanuel Vallée, Olivier Commowick, Christian Barillot, et al.. Unsupervised Domain Adaptation With Optimal Transport in Multi–Site Segmentation of Multiple Sclerosis Lesions From MRI Data. Frontiers in Computational Neuroscience, Frontiers, 2020, 14, pp.1–13. ⟨10.3389/fncom.2020.00019⟩. ⟨hal–02317028v2⟩
• Titouan Vayer, Laetitia Chapel, Rémi Flamary, Romain Tavenard, Nicolas Courty. Fused Gromov–Wasserstein distance for structured objects: theoretical foundations and mathematical properties. 2019. ⟨hal–02174316⟩ . Accepted for publication in Algorithms
• Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia. Optimal Transport for Multi–source Domain Adaptation under Target Shift. 22nd International Conference on Artificial Intelligence and Statistics (AISTATS) 2019, Apr 2019, Naha, Japan. ⟨hal–02082874⟩
• Kilian Fatras, Younes Zine, Rémi Flamary, Rémi Gribonval, Nicolas Courty. Learning with minibatch Wasserstein : asymptotic and gradient properties. AISTATS 2020 – 23nd International Conference on Artificial Intelligence and Statistics, Jun 2020, Palermo, Italy. pp.1–20. ⟨hal–02502329⟩
• Ievgen Redko, Titouan Vayer, Rémi Flamary, Nicolas Courty. CO–Optimal Transport. Neural Information Processing Systems (NeurIPS), Dec 2020, Online, Canada. ⟨hal–02972087⟩
• Chapel, Laetitia, Mokhtar Z. Alaya, and Gilles Gasso. "Partial Optimal Transport with Applications on Positive-Unlabeled Learning." Neural Information Processing Systems (NeurIPS), Dec 2020, Online, Canada. arXiv:2002.08276 (2020).

Preprints

• Cédric Vincent–Cuaz, Titouan Vayer, Rémi Flamary, Marco Corneli, Nicolas Courty. Online Graph Dictionary Learning. 2021. ⟨hal–03140349⟩
• B. Damodaran, K. Fatras, S. Lobry, R. Flamary, D. Tuia, N. Courty. Pushing the right boundaries matters! Wasserstein Adversarial Training for Label Noise. 2019. https://hal.archives-ouvertes.fr/hal–02174313
• Alain Rakotomamonjy, Abraham Traore, Maxime Berar , Rémi Flamary, Nicolas Courty , 'Wasserstein Distance Measure Machines', arXiv:1803.00250