TP2: Fonctions Récursives

Définir récursivement les fonctions pair et impair. On suppose que l'argument de ces fonctions est positif ou nul. Vous ne devez pas effectuer de division par 2, mais utiliser la fonction prédéfinie prédécesseur pred.

val pair : int -> bool = <fun>
val impair : int -> bool = <fun>

1. Définir une fonction sigma qui reçoit en argument un intervalle \([a,b]\) d'entiers représenté par un doublet et rend la somme des entiers appartenant à l'intervalle. Renvoyer \(0\) si \(a > b\).

   val sigma : int * int -> int = <fun>
   

2. Définir une fonction sigma2 qui reçoit en argument une fonction f, un intervalle \([a,b]\) d'entiers représenté par une paire, et rend la somme des valeurs de la fonction pour chaque entier appartenant à l'intervalle.

   \[sigma2\;f\;[a,b] \quad = \quad \sum_{n=a}^b f(n)\]

   val sigma2 : (int -> int) -> int * int -> int = <fun>
   

3. Nous allons maintenant généraliser. Plutôt que de choisir un intervalle nous allons donner une valeur de départ, une valeur de fin (pas forcément atteinte exactement, on continue tant que l'on est inférieur ou égal à cette valeur) et une valeur d'incrément. Plutôt que de faire une somme, nous allons utiliser une fonction de cumul fc et une valeur initiale pour le cumul acci. Définir cette nouvelle fonction sigma3 dont le type inféré est

   val sigma3 :
     (int -> 'a) -> int * int * int -> ('a -> 'b -> 'b) * 'b -> 'b = <fun>
   

   et dont la sémantique est spécifiée par : \[ sigma3\;f\;(a,b,i)\;(fc,acci) \; = \; fc \; (f\; (a+n*i)) \; (\cdots fc \; (f (a+i))\; (fc\; (f a)\; acci) \cdots) \] ou de manière graphique :

   

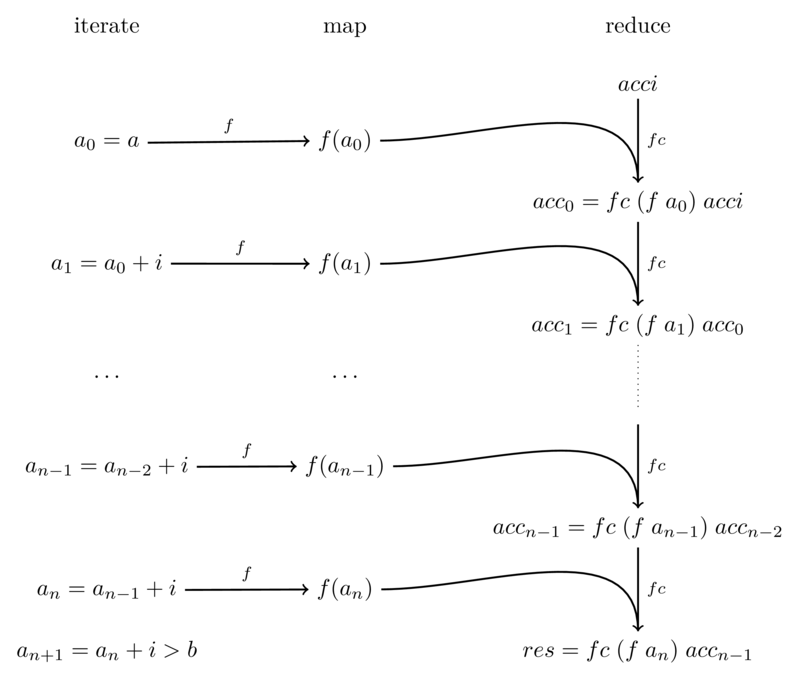
   Tester avec cette application qui accumule les résultats dans une liste:

   let res = sigma3 (fun x -> x * x) (0,10,2) ((fun x acc -> x :: acc), [])
   

   val res : int list = [100; 64; 36; 16; 4; 0]
   

4. Plus général encore : la fonction précédente ne permet pas de cumuler des valeurs quelconques. Plutôt que de fournir une valeur d'incrément nous allons fournir une fonction, et plutôt qu'une valeur de fin un prédicat d'arrêt. Définir donc la fonction sigma4

   val sigma4 :
     ('a -> 'b) ->
     ('a -> bool) * ('a -> 'a) -> ('b -> 'c -> 'c) * 'c -> 'a -> 'c =
     <fun>
   

   utilisée comme suit

   sigma4 f (predarret, fctincr) (fc,acci) a
   

   en commençant par a, tant que predarret retourne faux, appliquer f à a et accumuler le résultat dans acci avec fc. Continuer ensuite avec la valeur suivante, donnée par fctincr appliquée à a.

5. Utiliser sigma4 pour définir une fonction de cumul cum sur un intervalle flottant \([a,b]\) avec un pas \(dx\).

   val cum :
     (float -> 'a) -> float * float * float -> ('a -> 'b -> 'b) * 'b -> 'b =
     <fun>
   

6. Utiliser cum pour définir une fonction integre d'intégration numérique sachant : \[\int_a^b f(x) dx \quad \approx \quad \sum_{n=0}^{n=\lfloor \frac{b-a}{dx} \rfloor} f(a+n dx)dx\]

   val integre : (float -> float) -> float * float * float -> float =
     <fun>
   

   Utiliser integre pour approcher \(\int_1^2 \frac{1}{x}dx\).

Considérons une fonction continue \(f\) ayant un maximum local unique sur l'intervalle \([a,b]\) et n'étant jamais constante sur un sous-intervalle de \([a,b]\). Nous nous intéressons au calcul du maximum de cette fonction sur l'intervalle \([a,b]\) . La méthode s'appuie sur l'idée suivante : soient \(x\) et \(y\) deux points de l'intervalle \([a,b]\) tels que \(x < y\). Si \(f(x) > f(y)\) alors le maximum se situe dans l'intervalle \([a,y]\), tandis que si \(f(x) < f(y)\) le maximum est dans l'intervalle \([x,b]\). Définir une fonction maxi qui reçoit en argument une fonction \(f\), un intervalle \([a,b]\) et une précision \(p\) et calcule le maximum \(f\; m\) de \(f\) sur cet intervalle \([a,b]\) de telle sorte que \(m\) soit déterminé avec une précision \(p\). Attention, il faut retourner \(f\;m\) et pas \(m\). Penser aux définitions locales et tester.

val maxi : (float -> 'a) -> float * float -> float -> 'a = <fun>

Si l'on suppose que le générateur aléatoire de OCaml est uniforme et que l'on fait deux tirages aléatoires x et y entre 0. et 1., alors la probabilité que \(x^2 + y^2 \leq 1\) est égale à \(\pi / 4\). Intuitivement, x et y représentent un point dans un carré de côté \(1\), et si \(x^2 + y^2 \leq 1\), alors le point est dans le quart de disque centré en \((0,0)\) et de rayon \(1\).

Écrire une fonction montepi n qui tire n points au hasard et donne une approximation de \(\pi\). On pourra se servir le la fonction Random.float f qui retourne un nombre flottant au hasard compris entre 0. et f.

val montepi : int -> float = <fun>

let pi = montepi 1000000

val pi : float = 3.14254